Why people prefer simple, explainable models (Part 8)

(This post is part of a series on working with data from start to finish.)

Models, by their very nature, do not represent all of reality, but just the parts we seek to understand. All models are reductive, compressing reality into a finite set of comprehensible parts. The number of parts in a model corresponds to the model’s parsimony.

In a mathematical model, parsimony is the number of terms in an equation. In a statistical model, it is the number of parameters. In a schematic, it is the number of discrete components. In a sentence, it is the number of “things” described.

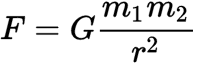
Image credit: Author’s own work

The set of properties (or components) which uniquely describes an entity - including a model - is given by its unique key, which therefore implies that a model’s parsimony is analogous to its resolution, as well as its line of representation.

A model with fewer parts features a shorter unique key, greater parsimony, coarser-grained resolution and more detail abstracted beneath its line of representation. In contrast, a model with more parts features a longer unique key, lesser parsimony, finer-grained resolution and more detail visible above its line of representation.

Parsimony as intelligibility #

Parsimony renders the ways in which things operate intelligible. If you explain to someone how all of economics works with thousands of little details, it will be less intelligible than an alternative explanation emphasizing only “the big picture”, such as the mechanics of supply and demand. Similarly, describing the motion of each individual atom in a room would be inscrutably complex, but summarizing their collective movement as “temperature” would be concise and comprehensible.

Of course, there is no cosmic guarantee that everything in the universe must be simple and parsimonious enough for humans to understand. It is absolutely possible to have accurate models of reality which are virtually impenetrable to the vast majority of people (take the Krebs cycle), and with the rapid ascendance of machine learning models, this will increasingly become the case. While we tolerate such models, we do so reluctantly, often deriding them as inelegant, complicated and ugly.

To change a system, you need handlebars #

Parsimonious models have clear handlebars.

If I tell you that, to improve sales on a retail website, you need to consider each individual user’s demographics, the time of day, all historical changes to their shopping cart, the sequence of clicks on every page and so on, it is not so obvious which of these things you should actually intervene upon.

If, instead, I tell you that you should just focus on getting a user to view their first product, it is far more apparent where to start.

It is almost certainly the case that the latter model is less accurate - after all, R² can only decline with fewer terms - but because it is more parsimonious, it is also more actionable. A model with too many moving parts is not actionable; a model synthesizing with just the main takeaway is.

Must we sacrifice accuracy for the sake of parsimony? Not always, which brings us to the topic of scale.