Data processing, from instrument to analytic resolution (Part 5)

(This post is part of a series on working with data from start to finish.)

Although our instruments should be maximally sensitive, accurate and precise, such a prescription does not offer much guidance as to what we should do with the data once we collect it.

In particular, we run the risk of “information overload.” Maximal resolution, and thus maximal observability, is achieved by recording additional properties or sampling more frequently. In both cases, this means more data - a lot more. A single computer tracking 10 4-byte properties every second will produce 2.4kb per minute; 100 computers tracking 20 properties sampling every tenth of a second would produce 4.8MB per minute. This is considerably more data to store and query.

Nevertheless, the costs of capturing, storing, retrieving and processing data have plummeted since the advent of “big data” in the 21st century. Just decades prior, you needed a physical person to record individual measurements in a notebook, a physical “data room” in which all measurements were stored and centralized, and a data analysis process that utilized no reproducible code.

As a result of subsequent technological advancements in data storage and processing, this entire data pipeline has become dramatically cheaper and more efficient. Today, you can log generously throughout your codebase with virtually no performance penalty, store that data within a logging service and data warehouse, fetch it with read-optimized queries, and aggregate it into sophisticated analyses using massively-parallel processing (MPP) and real-time data visualization. The resulting frictionlessness of data processing has catapulted the phrase “add more logs” into the firmament of distributed software debugging. We can, and do, collect more data than we ever have in history.

How do we make sense of it all?

Instrument resolution and analytic resolution #

We do the same thing we have always done: we process the data. Simply looking around you at this very moment, you will find an overwhelming amount of information - more than you could ever make sense of or act upon. Although a tremendous amount of information is available, it is not all necessarily relevant. As if smelting iron into steel, we must process data into a more comprehensible and relevant form before it is put to use.

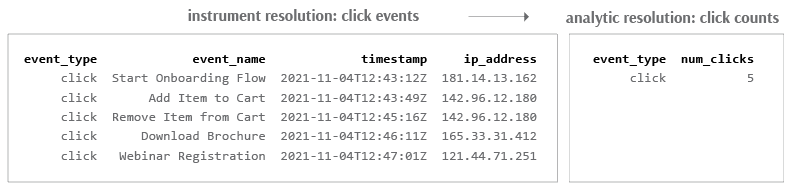
Here it is useful to distinguish between instrument resolution, or the unit of observation, and analytic resolution, or the unit of analysis.

At the level of instrumentation, we want to collect as much data as possible - that is, at the most granular resolution. This offers us the potential of completely knowing our environment. In practice, however, most of this information is not relevant to us, and so we ignore it. What we keep, we process and analyze.

This analysis invariably occurs at a coarser resolution than that of our instrument. As with instrument resolution, analytic resolution also has a “line of representation” (commonly called a “layer of abstraction”), and this too is defined by the unique key. Things below one layer of abstraction are invisible (at this level of analysis), while things above it are visible. In particular, analytic resolution intentionally obscures all irrelevant detail below the level of abstraction, leaving only the most high-level patterns to analyze above it.

By construction, there are always fewer high-level patterns than low-level details because it is easier to pattern-match on a few, high-level units of analysis than millions of units of observation. By convention, we refer to these processed, refined, high-level outputs as “abstractions”.

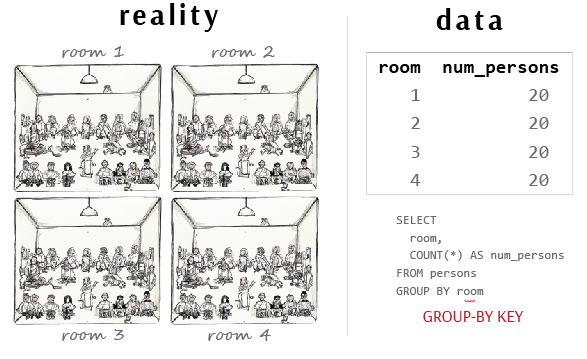
For example, if we want to count the number of people in a room, we have reduced all underlying information about these individuals - each with their own idiosyncrasies - into a single data point. For the purposes of our count, everything else about these individuals is irrelevant. If we imagine four rooms like this, and we want to know how many people are in each room, we can see that our analytic resolution corresponds to the “room-level”, beneath which any detail about individuals remains invisible and indistinguishable.

Analytic resolution as a GROUP BY statement #

Just as our instruments capture data at the granularity of the unique key, our analysis similarly aggregates the data at the level of the “group-by key.” In SQL, this refers to the set of properties which uniquely identify a unit of analysis and upon which aggregations (such as sum, average, max, min) are performed. In the prior example, calculating the total number of people in a single room has no group-by key, while calculating the number of people within each room would have a group-by key at the room-level. Besides aggregation, other methods of data processing commonly include filtering (the “where” clause in SQL) and transformation (such as log-transform, mapping and concatenation).

Above the line and below the line of analytic resolution #

The invisibility of “irrelevant” detail stemming from too high a level of resolution can lead to predictably disastrous consequences. Imagine I ask you to count how many men and women are in a crowded room. You count 56 women and 44 men. Does this really reflect reality as it is? What about people who identify as non-binary or cross-gender? In fact, what inevitably occurs when we discretize reality for the purposes of data collection is that we “bucket” individuals into the closest available category and obscure “irrelevant” details below it. It does not mean these details do not exist, only that they are excluded from data collection: we do not “see” them.

Or consider the binary digits upon which our computers operate. Do our computers truly manipulate discrete 1s and 0s? They do not. The transistors powering our computers in fact measure voltage, the difference in electric potential between two points on a circuit. When a transistor detects a voltage between .2V and .8V, it encodes a “0”, and between 2V and 3.5V, a “1”. Despite there being more information (i.e. a greater range of values) in the original voltage signal, this information is reduced (or “quantized”) to the more practically useful form of 0s and 1s for their subsequent use in Boolean algebra.

The ineluctable subjectivity of discretization #

It is sometimes believed that data is impartial, or at very least, can be impartial. After all, data appears to record observed facts about the world as they are. It is worth clarifying that while data can be unambiguous, it can never be unbiased. Data always includes assumptions by the operator analyzing data or the instrument collecting data about (1) what the level of resolution is, and therefore what properties are recorded, (2) what qualifies as “valid” values within those properties, and (3) how individual observations are bucketed into the “nearest” value.

One can imagine, for example, a government form that (1) collects gender information, (2) accepts valid values of “male”, “female” and “other”, and (3) coerces individuals to use either of those 3 values. Similarly, a digital computer (1) operates using the binary digit, (2) accepts valid values of 0 and 1, and (3) coerces digital voltages into either of those two values. None of these categories or assignments exist naturally; all are designed into the data collection and analysis process.

Choosing an analytic resolution for observability and with handlebars #

Given that one can vary analytic resolution by zooming in and out of various levels of abstraction, or alternatively by modifying the group-by key, which analytic resolution do you ultimately choose? Generally speaking, you should choose the level of resolution required to see the problem you are trying to solve. If you are tackling the growing amount of pollution in cities each year, you will fail to see relevant patterns when analyzing pollution data hour-by-hour. You will instead see too much noise, too much low-level variability. You need to zoom out. However, because the full view of a problem is rarely clear from the outset, you need to explore multiple levels of analysis in order to see the problem clearly. As if varying the magnification on a microscope, you change your analytic resolution to see if a problem slides into focus or fades into blur.

Seeing a problem is one thing; fixing it is another. Just because you see a problem at one level of resolution does not mean you can act on it at that level. In fact, almost always, you will notice a problem at a high level of resolution (a program crashes), then concretely fix it at a lower level of resolution (the actual lines of code). The same is true for data analysis generally. While we may find one level of resolution brilliantly illuminates the problem we are observing, we must invariably drill down into the details to identify what we can actually change.

In practice, there are many things we cannot change for legal reasons, technical reasons, risk reasons or ethical reasons. These constitute constraints. Our job then is to find entry points into our problem: alternative routes which solve our problem while still respecting its constraints. Ultimately, the level of resolution along which we make changes should have “handlebars”: clear next steps in the form of product changes, marketing campaigns, sales tactics and so on. Without handlebars, we can merely observe a problem without ever orienting ourselves toward fixing it.

Precision, accuracy and resolution for analytical data #

Finally, like the unit of observation, the unit of analysis can also be described by its precision, accuracy and resolution.

Data analyses which are unstable over consecutive runs, due to changing data or changing logic, will invite questions around precision. Data analyses which contradict the results of other systems or practitioner intuition will invite questions around accuracy. And data analyses which operate at the wrong level of resolution, either because they do not illustrate the problem or because they do not demonstrate concrete next steps, will invite questions around resolution (i.e. analytical relevance).

Just as with collecting data, we therefore always seek to maximize precision, accuracy and resolution when processing and analyzing data.