How do we know if data is "correct"? (Part 3)

(This post is part of a series on working with data from start to finish.)

As our instruments collect information about the world, we in turn expect them to represent that information accurately. If we move a thermometer from indoors to outdoors on a cold, winter day, we expect the measured temperature to fall. If it does not, we may quickly surmise that the thermometer’s reading is incorrect and that the thermometer is not working properly.

Accuracy, however, is a vexingly complicated philosophical problem. If you’ve ever harbored doubt about a certain analysis or chart or reported set of data, you have run into the pervasive problem of “inaccuracy”. As if tranquilizing an elephant, such doubts can paralyze data operations at organizations of virtually any scale.

Although the word “accuracy” is traditionally used to denote the correctness of a measurement, the International Organization for Standardization (ISO) no longer uses this term.

Instead, they use trueness, defined as the agreement between a measured value and the “true or accepted reference value” (ISO-5751:1994, 0.1). Accuracy, according to ISO, consists of both (1) trueness and (2) precision. Despite these definitions however, the term trueness is not yet widely used, so I will continue to use accuracy and correctness interchangeably for the purposes of this essay.

Consider the following popular optical illusion. Are the lines between the arrows of equal length?

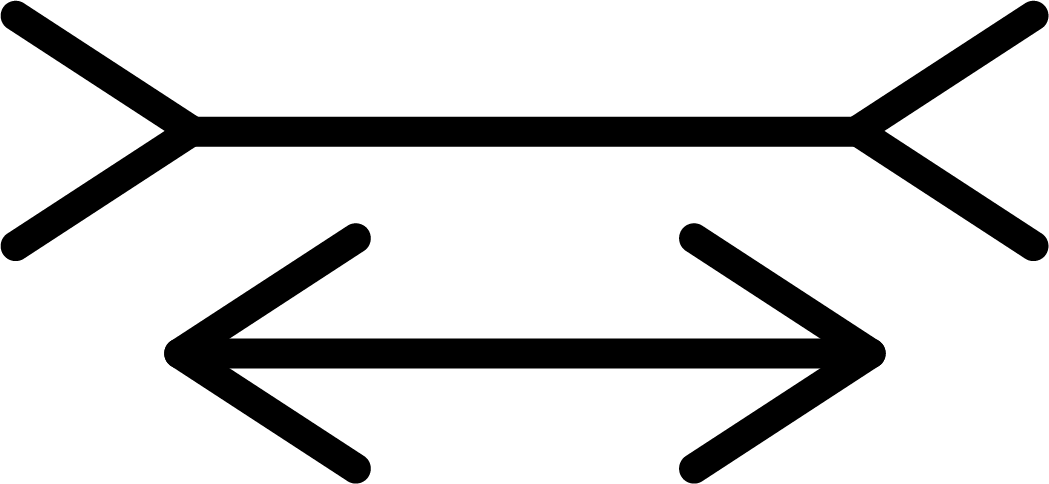
Image credit: Author’s own work

It may appear as though the top line is longer than the bottom line. In reality, however, the lines are equal in length.

Here I have proposed two mutually incompatible descriptions of the world: one where the two lines are unequal, and the other where they are. These two descriptions - in data terminology - “fail to reconcile”. Which is correct?

Both perspectives are modestly convincing. In the former, your eyes tell you the top line is longer. In the latter, I am telling you that both lines are equal. You admit that your eyes can be deceived and trust this is a popular optical illusion for good reason, so you opt to believe the latter claim over the former.

Notice that the most reasonable proposal is considered “correct”; alternative proposals are summarily dismissed. This does not mean we have actually arrived at the correct answer, only that we have mapped the most reasonable answer to being the provisionally correct one. (Now consider if I told you that in fact I modified this image so that the lines are not equal in length - were your eyes correct all along?)

What then does it mean for something to be “correct”?

It means there exists some logic, evidence or consensus which makes a reasonably persuasive claim about the “true” state of the world.

If there exist multiple and potentially contradictory claims about the true state of the world, then it is not immediately clear which side is correct. “Who” or “what” is correct can rapidly change depending on the strength of the arguments used to support such claims. The “evolution” of correctness over time, which hinges on the prevailing scientific consensus around particular theories, underlies Thomas Kuhn’s notion of paradigm shifts within the history of science.

Correctness as independent consensus #

Imagine you are counting the number of marbles on a table. You count 48. Because you counted a little carelessly, you are not completely sure. Is your initial count of 48 “correct”?

We may say it is provisionally correct, although a recount is recommended. There remains some uncertainty about the true number of marbles on the table. You count again and you get 48. For good measure, you count a third time and get 48 once more. By this point, you are fairly certain the true number of marbles on the table is 48.

Notice how the strength of the claim - that there are 48 marbles on the table - increases as a function of reproducibility. The first count of 48 marbles included uncertainty over the true amount of marbles, but by the third count, this uncertainty was reduced to virtually zero.

Because every subsequent count reconciled with the initial count, there was no variation (or “error”) across the series of measurements. The measurements were invariant over space and time. We may also say that this reproducibility represented a form of consensus: every recount agreed with the first. If, on the other hand, our estimates varied based on how we were feeling or what we were drinking, then they would be subjective and unreliable.

Imagine your friend now enters the room and you ask her to confirm your count of the marbles. She counts 49. Instantaneously, the correctness of your count has been thrown into question, as has hers. She counts again: 49. The correctness of your count is correspondingly diminished, and hers seems increasingly plausible

Image credit: DALL-E

What does this reveal? A consensus of independent opinions improves our confidence in the correctness of a value. A divergence in those independent opinions diminishes our confidence in all of them. More independent opinions are better than one, but only if they converge. If, from every possible facet of analysis or perspective, we always converge upon the same answer - that is, it is invariant over space and time - then we say it is objective. Objectivity, then, is a form of consensus achieved from multiple independent perspectives.

When ISO refers to the trueness of a measurement, they are conveying the same idea: it is the accepted reference value. ISO recommends this come from theory, prior experimental data, practitioner consensus or - absent those - the simple mean from a set of experiments (ISO 5725-1:1994, 3.5).

By this point, we might wonder: how many marbles are actually on the table? Currently it is “either 48 or 49” (at least until another friend adjudicates!), which is to say, indeterminate. We simply do not know the correct number of marbles until we gather more opinions or perform more recounts to shore up our collective confidence.

Correctness as a continuous variable #

As each of these examples demonstrate, correctness exists not on a binary spectrum of “true-false” but rather a continuous one of “reasonable-unreasonable”. If the correctness of your calculations are in doubt, you improve confidence by reconciling it with more independent opinions, be they alternative data systems, calculation methodologies, or even expert opinion. The more these converge, the more “correct” the calculation becomes.

Data analysts are often disappointed to discover how much of their day-to-day work involves remediating trivial data quality errors, retracing transformations applied to particular fields, or reconciling calculations between various data systems. Isn’t data analysis work about analysis, not reconciliation?

The reality is that without confidence in data correctness, only achieved through the successful reconciliation of independent evaluations, there is equivalently little confidence in subsequent analysis or understanding. Suspect data integrity jeopardizes the truth value of the entire data infrastructure, as well as any related systems in which it is used for reconciliation.

A robust data infrastructure therefore systematically and regularly reinforces the integrity of its data by way of reconciliation “checkpoints” throughout the data lifecycle: source to destination, calculation to calculation, system to system, and analysis to analysis.