What is a data record? Resolution and the unique key (Part 2)
(This post is part of a series on working with data from start to finish.)
Instruments observe, and the resulting measurements record, reality at a given resolution. Resolution reflects the degree to which an instrument can differentiate between two separate states of the world, or “states” for short. Those states may be spatial in nature, such as a marble which is either red or green, or temporal, such as a digital thermometer performing readings once per second.
If you look at the surface of a table, you will be unable to differentiate dust particles micrometers apart because the resolution of your eyes is too low to detect differences at that scale. Absent the ability to differentiate, these otherwise different specks of dust appear to be only a single thing. In other words, they are indistinguishable. The fact that these dust particles exist at a level of resolution higher than that of your eyes effectively renders their differences unobservable to you. If enough particles were to clump together within an entire millimeter instead of a micrometer, the dust would - like the tip of an iceberg emerging above water - suddenly become visible.
The more we increase the resolution of our instruments, the more we are able to differentiate between different “things”. The greater our resolution then, the more things there are. It is therefore by way of resolution that we are able to see and differentiate things at all. Resolution is the foundation of observability.
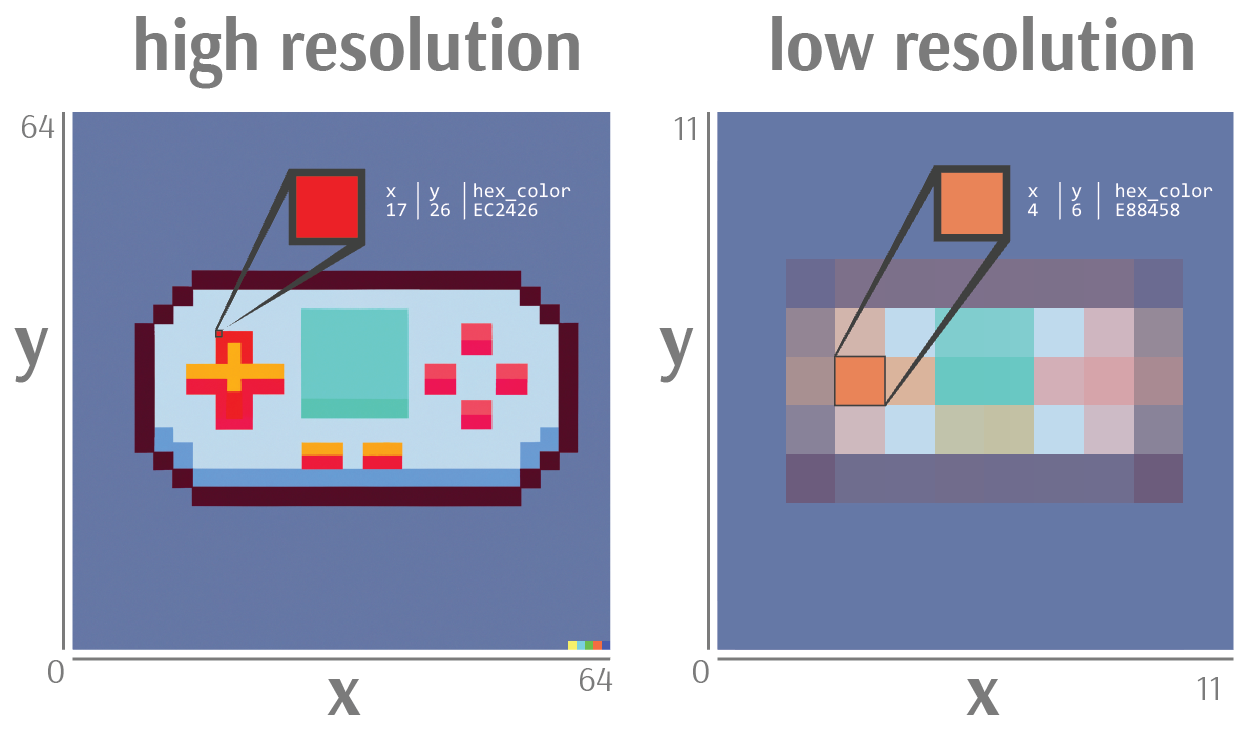
Image credit: DALL-E, author’s own work
“Above the line, below the line” #
The notion of an umwelt, or in German “one’s immediate surroundings”, is instructive. An umwelt refers to the phenomenology of your present experience: what do you perceive at this very moment? What do you see directly in front of you, or hear around you? Things behind you for example, which you do not physically perceive, are not within your umwelt. Your umwelt is a dynamic cone of sensory experience, shifting as you pivot your head, body and attention.
Borrowing a term from the late Dr. Richard I. Cook, we may refer to the outer shell of our umwelt as the “line of representation.” Like the cosmic microwave background, it reflects the absolute limit of our local, observable universe. Things beyond (or “below”) the line of representation are invisible to us - they cannot be represented. Only the bits of reality which penetrate our umwelt, demarcated by the resolution of our sensing instruments, become visible.
High-resolution instruments correspond to low lines of representation, meaning more details are observable above the line and fewer are unobservable below it. By contrast, low-resolution instruments obscure large swaths of reality below its high line of representation, sparing only a few details above it.
The unique key defines an entity #
Every observable thing, or entity, can be described by a set of properties, each of which can assume discrete values. For example, if you see a marble in front of you, you may describe it as “red” in color, “small” in size and “hard” in texture. Color, size and texture are properties which describe marbles generally, while red, small and hard are values which describe this marble specifically. If you observed multiple marbles and classified each of them in color, size and texture, you would gradually amass “data” about marbles.

Image credit: DALL-E, author’s own work
I must preemptively clarify the claim that entities can be reduced to a finite set of properties. Indeed, the world is too complex and rich in detail for this to be true. However, if we are to describe an entity, we must necessarily reduce it to a finite set of properties. It is not possible to describe an entity except by way of its discrete properties. Something either is a certain way, or it is not. A value equals pi, or it does not; a ruler is 12 inches long, or it is not. Discretization reveals more about the constraints of human reasoning than it does reality itself.
The set of properties which uniquely identifies any entity is its unique key. If two or more entities have identical values for all properties along the unique key, then those entities are not unique. They are instead redundant and otherwise indistinguishable from one another.
Returning to the example above, let’s declare that all marbles in the world - by definition - are defined by three and only three characteristics: color, size, texture. Imagine you then observe two marbles before you, both of which appear to be exactly the same according to our definition: they are both red, small and hard. These two marbles are therefore logically indistinguishable.
But, you object, you can visibly distinguish them as separate marbles! How can their properties be identical along the unique key, which would logically render them the same, and yet they are observably different? Certainly, at least, you can observe one on the left and one on the right.
In doing so, we have introduced another property called position. One marble’s position is on the “left”, the other on the “right”. Therefore, we have extended the unique key from [color, size, texture] to [color, size, texture, position]. If we can observably distinguish two separate things, then they must differ on at least one property of their unique key.

Image credit: DALL-E, author’s own work
The more capable we are at distinguishing two separate states of the world - that is, increasing our resolution - the more properties we append to our unique key. In other words, the unique key is identical to our line of representation. The greater the detail with which we observe the world, the longer the unique key becomes. The more coarse-grained our view of the world, the shorter the unique key gets. As with lines of representation, entities whose unique key exceeds that of our instruments remain stubbornly unobservable to us.
Resolution and data collection #
In virtually all telemetric systems, assuming data storage costs and data retrieval times are negligible, we want our instruments to perform measurements at the highest resolution possible. In software engineering, this is sometimes referred to as “log everything.”
Maximizing the resolution of our instruments is not some petty curiosity in ravenous pursuit of more information. It is the bedrock of scientific progress.
The greater our instruments can resolve phenomena at subatomic scales - only achievable by virtue of extraordinarily high-resolution instruments - the more we are able to empirically verify the predictions of physics. At the other end of the spectrum, the greater our instruments can resolve details of our vast cosmic universe, the more we are able to verify theoretical predictions about the evolution of the early universe. Finally, on a more familiar scale, the greater modern modems can resolve minute differences in an electromagnetic wave’s frequency, phase and amplitude, the more digital information we can encode onto that wave, thereby increasing network bandwidth.
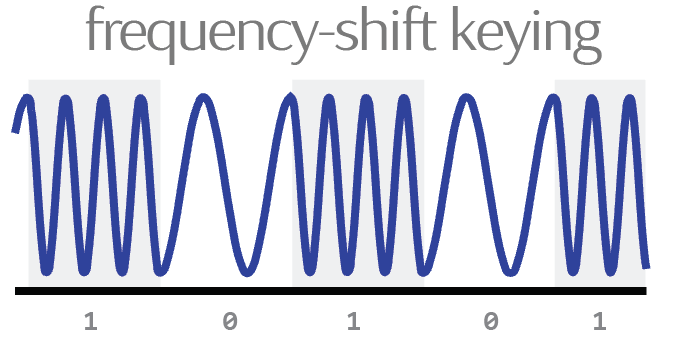
Image credit: Author’s own work
In practice, data storage costs and data retrieval times are not negligible. If you store a couple billion data points, it will take time to search for the couple thousand you are interested in. I will address the issue of “information overload” later in this series. For now however, we can assume we always want to maximize the resolution of our instruments because it offers us the most detailed, granular and comprehensive view of our operating environment.
Spatial and temporal resolution #
Practically speaking, how do we maximize the resolution of our instruments? We can decompose this into two parts:
- Resolution in space
- Resolution in time
To increase an instrument’s resolution in space, add more properties to the unique key. Returning to the example of the red, small, hard marble above, we may further describe its location as “on a table”, its manufacture date as in “2014”, its time of last observation as “now”, and so on. In doing so, we have developed a more detailed, fine-grained description of the marble, or equivalently have increased the resolution at which we record data.
To increase an instrument’s resolution in time, sample more frequently. The red marble may be gradually rolling down a small slope. I can record its position both at the beginning of the descent as well as at the end, yielding two data points. I can then increase the sampling frequency to record at the beginning and at the end, as well as ten times in between (each observation with its respective timestamp). In doing so, I have developed a more detailed, fine-grained description of the marble over time.
Expressed in tabular format, increasing our resolution in space creates a wide table of cross-sectional data, while increasing our resolution in time creates a long table of longitudinal data.
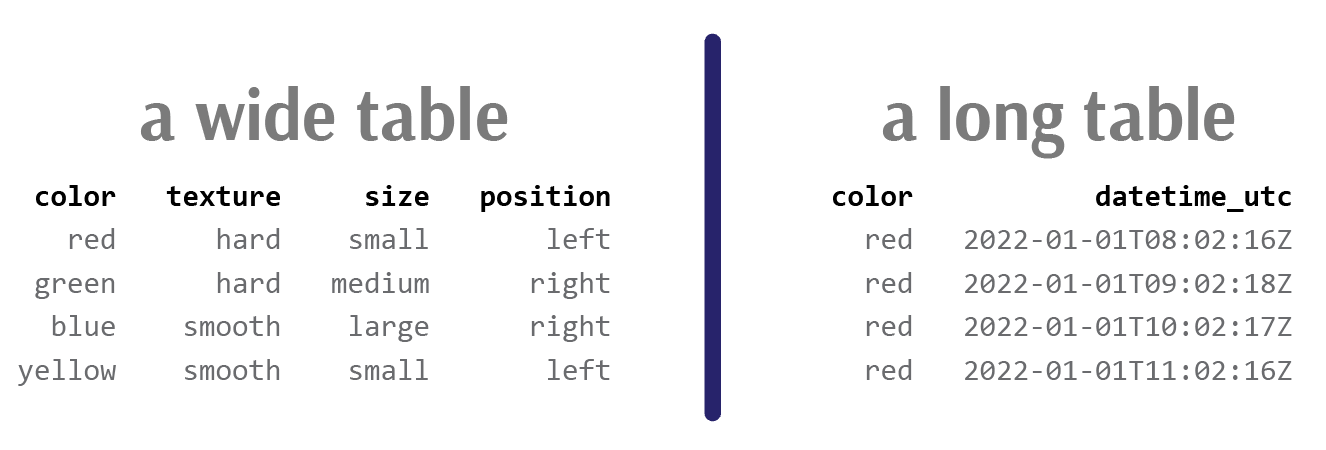
Image credit: Author’s own work