Statistics only gives correlations, so what about causation? (Part 11)

(This post is part of a series on working with data from start to finish.)

By this point, we have covered what data is, how it is collected, how it is processed, and how it is ultimately integrated into models of reality. When systems are working properly, we are completely disinterested in how they operate. But when they aren’t - when we are falling short in revenue growth or user engagement for example - we suddenly become captivated by the inner workings of a system. We wonder: how must we change this system to work more effectively?

In the simplest case, our model is entirely causal and deterministic: if we increase marketing spend over here, we will observe higher website impressions over there. In the more complex case, our model is correlational and non-deterministic: if we increase marketing spend over here, we might observe higher website impressions over there.

Naturally we prefer causal models to correlational ones as we are able to concentrate our resources on the actions which work and waste no effort on those which don’t. Causal knowledge, however, is very hard to come by. In fact, one might even argue that correlational knowledge is the best we can ever hope to achieve.

When first introducing models, we learned that theoretical models are entirely deterministic in nature. It is only upon validating their predictions against real-world measurements that we observe unexplained deviations from those predictions, or residuals, and therefore non-deterministic behavior.

As we improve our knowledge of a system by adding more detail (components), the previously unexplained behavior becomes increasingly explainable. Observations attributed to the systematic, deterministic components of our model (R²) rise while those attributed to the stochastic, non-deterministic component (random error) fall.

At the limit, all unexplained variation metamorphoses into explained variation, thereby producing an entirely deterministic model. What remains is equivalent to our notion of precision: a precise instrument is one that causally, deterministically and with no unexplained variation produces identical results under identical conditions.

We know from Heisenberg’s uncertainty principle that we can never possess complete knowledge of a system, and therefore can never eliminate all unexplained variation. The moment we measure a system, we exit the land of deterministic, theoretical models and enter that of incomplete, statistical models. We are ejected from the realm of causality and relegated to that of correlation.

Can we nevertheless extract causality from causation?

I would argue that, theoretically, we cannot. Practically speaking, however, we frequently settle for “very, very convincing correlations” as indicative of causation. A correlation may be persuasively described as causation if three conditions are met:

1. Completeness: The association itself (R²) is 100%. When we observe X, we always observe Y.
2. No bias: The association between X and Y is not affected by a third, omitted variable, Z.
3. Temporality: X temporally precedes Y.

For example, consider knocking a glass of water off a table (X) and subsequently observing the water on the floor (Y). If we were to knock the glass off multiple times, we would always observe water on the floor: an R² of 100%. Similarly, although we cannot control for every other factor that might have caused water to land on the floor, it seems likely none of them interposed themselves between our knocking of the cup and the water on the floor. Finally, we note temporally that knocking the glass preceded spilled water on the floor. The relationship between X and Y is causal because, in a hypothetical world where we did not knock the glass off the table, we would correspondingly not observe water on the floor.

It is worth mentioning that temporality is only present in conventional notions of causality but is absent from classical physics. Known as T-symmetry or time reversibility, the laws of physics do not distinguish between past and future: they work backwards just as well as they do forwards. Only determinism (complete model fit) is required by physical theory.

The perception of time is typically ascribed to the second law of thermodynamics: in a vacuum (or within the universe as a whole), entropy only rises. This means the future is less predictable than the past. By contrast, complete model fit renders the future more predictable than the past. It might therefore be argued that the arrow of time is synonymous with entropy rising while the arrow of knowledge is synonymous with entropy falling[0].

What about the second condition, that of no bias? What if something outside of our model is influencing the outcomes we observe?

Imagine you are evaluating the effect of childhood lead exposure on a host of future life outcomes. If you were to build a model regressing such life outcomes on childhood lead exposure, you might indeed find a statistically significant, negative relationship. But does this mean childhood lead exposure causes those negative outcomes?

No. It is possible that children exposed to lead early on in life are also exposed to poor nutrition or poor education or poor air quality or poor financial circumstances, and it is these factors (confounds) which cause worse life outcomes. Unless we control for every possible factor (including many more not specified above) that could affect life outcomes while varying only the variable of interest - childhood lead exposure - we will have inadvertently introduced the possibility of omitting a causal factor from our model, or equivalently introducing “omitted variable bias.”

This is why statisticians regularly clarify that such a regression can only demonstrate “a relationship” or “an association”, but never, ever causation. When we fail to incorporate every possible factor that could affect what we are measuring, at least one of those “omitted variables” always remains a causal possibility.

The notion that our model could be systematically and explainably wrong is known as bias. Recall that, in a statistical model, there are three components which contribute to observed outcomes: systematic factors, systematic error (bias), and random error (imprecision). As we enrich our model with more detail, we shift variation explained by random error into that explained by systematic factors, thereby improving model fit (R²). But what about bias?

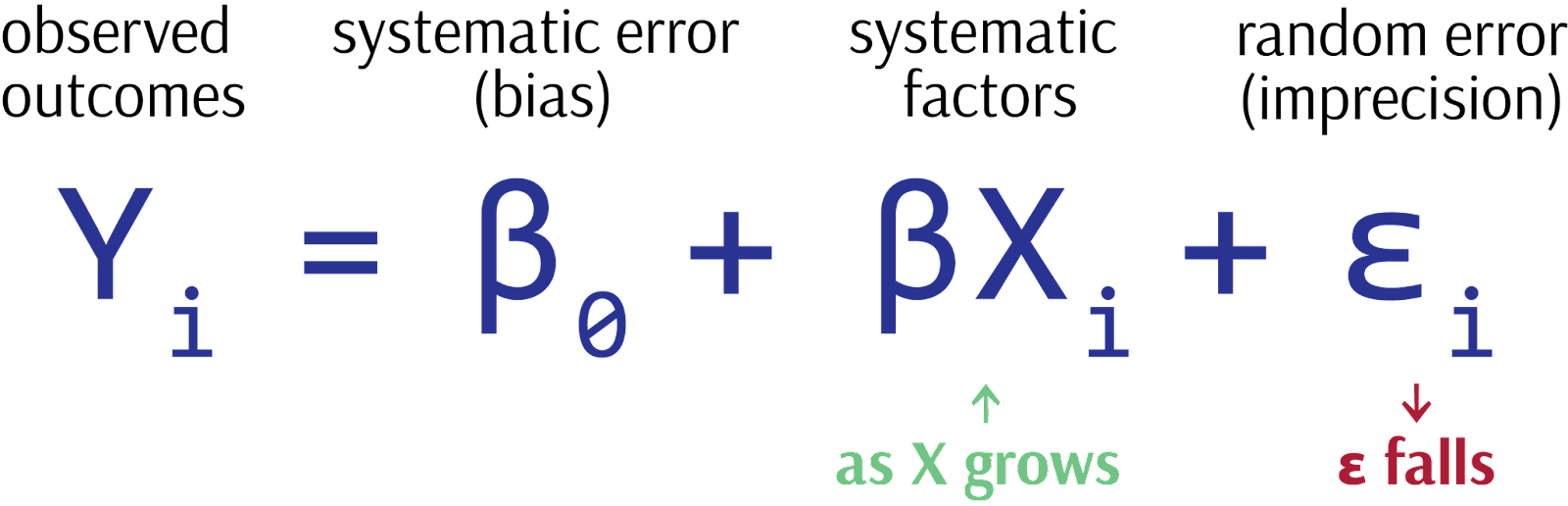
Image credit: Author’s own work

What do we do when our models are not unexplainably inaccurate (imprecise), but explainably inaccurate (biased)?

Statistical models do not address such bias. Tautologically, a model is only aware of what is included in the model, and not what is omitted from it. A model therefore cannot ensure that the model itself is not systematically biased.

Scientific procedures, on the other hand, can reduce this bias, the most notable of which is the scientific experiment. Unlike statistical models, which work with observational data (data created under conditions we passively observed), experiments produce experimental data (data created under conditions we actively controlled). Observational data is found; experimental data is created.

Experiments, and in particular randomly controlled trials (RCTs), operate by assigning participants (or “experimental units”) to a treatment group and a control group at random. By virtue of randomization, these groups in aggregate must be identical to one another but for the intervention applied only to the treatment group. The only way the average outcomes between these two groups can possibly differ is if the intervention truly had a causal effect.

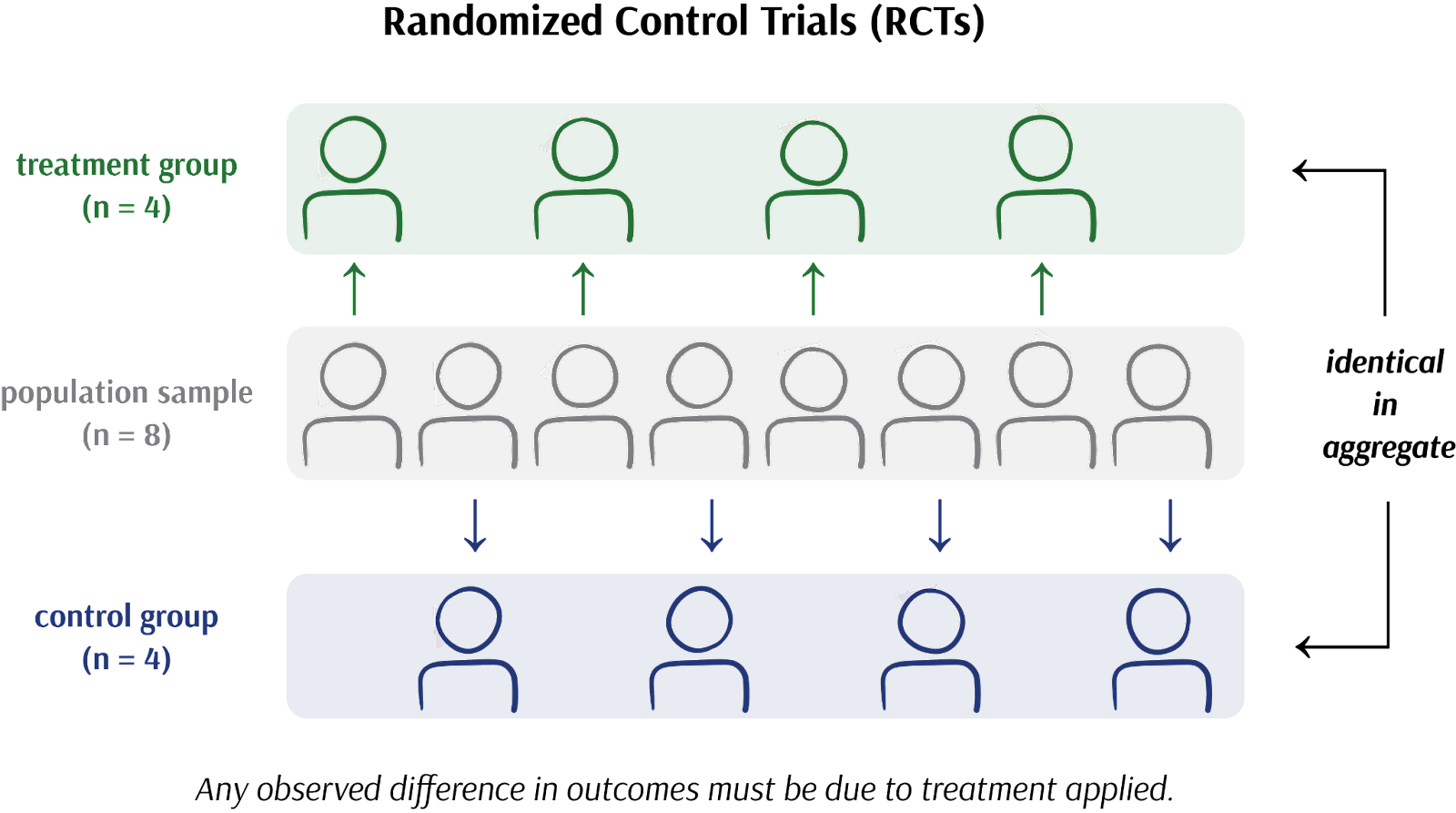
Image credit: Author’s own work

This approach to deducing causality, first clinically introduced in the 1930s on tuberculosis patients and now referred to as the Rubin Causal Model (RCM), quickly became the gold standard for scientific research in the 20th century. It equally became the foundation of commercial research in the 21st century, popularized by digital and massively scalable “A/B tests.”

The Rubin Causal Model is not perfect: after all, it can only deduce a rather handicapped version of causality. We cannot talk about causality amongst individuals, but instead only amongst populations.

It is not only possible, but in fact probable, to see “causal” effects in aggregate that do not apply to individuals. If a clinical research study claims a “mean improvement of 4%”, it means exactly that: an improvement across an average of individuals. However, there almost certainly exist individuals where it had no effect or even an adverse effect.

Despite its drawbacks, causal knowledge in aggregate is still often preferred to correlational knowledge. When we have the resources and expertise to run experiments, we should. When we don’t, we often instead settle for “indicative correlations” and their attendant caveats.

--

[0] Read Stephen Wolfram’s 3-part treatise on the Second Law of Thermodynamics for a more thorough investigation of entropy, the observer’s knowledge of a system, and computational irreducibility.