Complex systems

Hey all -

+ what I learned or rediscovered recently #

* Complex systems

We’re familiar with what normal systems are, which are simply collections of parts whose unified whole can do something that no individual part can do alone. Your phone, for example, is composed of many parts - a CPU and software and sensors - but none of them offer the complete, holistic functionality that your phone does.

Now, with many systems, we can inspect them and see how the parts relate to the whole. If I press down on the horn of a car, I know the car will honk. And I can do that 100 times and it will honk 100 times. This is a predictable, “orderly system.”

But there are many systems out there which are completely unpredictable. If I drop a feather from a building, or release a balloon into the wind, I have no idea where either will end up. Small changes in starting conditions compound as time goes on, creating the appearance of random behavior. In the mathematical sense, these are “chaotic systems.”

Here’s where it gets interesting: there are also systems which exhibit behavior of both orderly and chaotic systems. The stock market, the economy, international politics, technological innovation, natural selection, human behavior and so on - these are all examples of “complex systems.” Chance plays a fundamental role in outcomes, yet we can also spot orderly patterns emerging over time.

Complexity seems to oscillate between order and chaos. Just when we think we’ve identified a pattern or model or theory, the whole thing gets shaken up. Complex systems defy predictable, tractable and concise explanations.

There is no one, single definition of “complex systems”[1], but almost invariably, the study of complex systems concerns the study of networks. Complex systems tend to be tightly interconnected, which means they have a high network density.

Network density is a measure of how many relationships there are in the system. More specifically, it’s the amount of actual relationships in a system, divided by the maximum possible number of relationships in that system (formula: n * (n-1) / 2).

So an orderly system - low network density - may look like this:

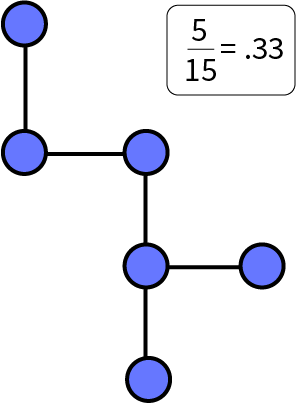
While a complex system - high network density - would look like this:

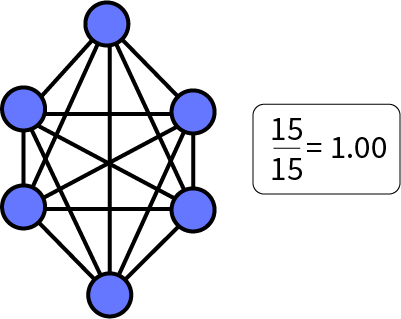
This would describe parts of the economy[2], social media or even the human brain, which are each composed of billions of interconnected parts. But it would not describe something like your car’s horn, which is interfacing at most with a few other parts. By this logic, a system then becomes more complex as it approaches the state of “everything is connected to everything.”

That’s neat and all, but what’s so important about complex systems? Well, they behave entirely differently from normal systems. Suddenly we see:

• Non-linear outcomes: little changes add up until they hit a “criticality point,” whereafter they jump violently

• Feedback loops: a little change ricochets around the network - amplifying along the way - until it circles back to where it started

• Emergent order: sometimes drastic changes lock the system into a new “regime” or “era,” such as the French Revolution or The Great Depression

• Chaotic behavior: there is an abject inability to predict outcomes in the future

OK - too much jargon. Each of these merit a deeper review in their own right, and I hope to do that in a future newsletter. But the main thing I want to emphasize is: if we’re dealing with highly networked systems, these phenomena are to be expected.

We should not be surprised when a piece of fake news goes viral, or when a stock market crash avalanches into a full-blown recession. Nor should we be surprised when things don’t work “as expected.” In complex systems, paradoxically, the only thing to expect is the unexpected.

And to the extent that there are complex systems in whatever our field of study is - be it biology or finance or sociology - we should expect these phenomena to be there as well. Complex systems are everywhere - the only question is how complex they are.

+ parting thoughts #

The study of complex systems is relatively recent, in part I believe because complex systems are simply more relevant than they were hundreds of years ago. Really since the telecommunications revolution, the world has become much, much more networked. Which also means the world has become much, much more complex.

That means we not only get less predictability over what will happen in the future, but when the unexpected does happen, it is more severe and non-linear in nature. The downside exposure here - in both risk and magnitude - led to the rise of reliability engineering and resilience engineering. How do we keep systems running, and what do we do if they fail?

On the other hand, I think complex systems should work both ways. They should work for us just as much as they work against us. If catastrophe is what happens when complexity goes wrong, then perhaps serendipity is what happens when complex systems go right.

Probably the best essay on complexity working for us was written by Kevin Kelly, who championed the rise of networked systems. He knew that complexity could go right, and if you harnessed that potential, you could have those complex phenomena work for you, not against you. And perhaps most impressively, he wrote that back in 1998.

Thanks for reading,

Alex

[1] As Dave P. noted, it’s important to distinguish between complex systems and complicated systems. A “complex system” is a technical term with a certain set of properties, whereas a “complicated system” may be any system which is simply hard to understand.

[2] I write “parts of” because analyzing any system depends on our level of analysis. For example, predicting the temperature of a system is far easier than predicting where any one molecule in that system will be.