For alpha, be informed and risk-seeking; otherwise, stick with beta

The world we live in is a fundamentally uncertain one.

Consciously and unconsciously, we are constantly evaluating probabilities and determining the outcomes which are most likely to occur. What time will my friends arrive at the bar? What will people think if I wear this? What kind of bar will this be, and will I enjoy it?

Financial practitioners and theorists have been studying uncertainty for centuries because it largely governs how much money they can expect to make - or lose - on their investments. They call this uncertainty risk, and it’s roughly measured by the difference between the best outcomes and the worst ones.

For example, what could happen when I try to sell my house? If it’s a seller’s market, I could sell it for 30% more than I bought it, but if it’s a buyer’s market, I may be forced to sell it at a 10% loss. As soon as I put it on the market, I really don’t know whether it will sell at +30% or -10%.

On the other hand, if I’m certain that I’m selling into a buyer’s market, there’s a narrower range of outcomes. Perhaps I can only sell it for a loss between 10% and 15%, with absolutely no chance of a gain. And despite losing money, there’s actually less risk than before because I’m far more certain about the price I’ll get.

risk in the real world #

Naturally we want the highest certainty of the getting the best outcome. Low risk, high return.

But these opportunities don’t last long. Everyone wants them, so they get snapped up. This leaves us with all the other opportunities, which offer less certainty and a wider range between good and bad outcomes.

In a competitive market, the only opportunities which remain can’t be “good deals” - someone would have gotten them already - instead they must be “fair deals.” They offer a decent chance at high returns, but only if we embrace the possibility of getting low or negative returns. In practice, risk is proportional to return. The higher you fly, the further you’ll fall.

At the same time, intuitively we’re fairly certain that good deals do exist. This job offer is a once-in-a-lifetime chance, or that investment opportunity is too good to pass up. In these cases, we’d want to engage our time, money and energy wholeheartedly into these because they appear to offer upside with little downside.

But here comes the paradox:

1. If these are good deals, we reap the benefits from seizing the opportunity.
2. If these turn out to be only fair deals, we actually took on a lot more risk than we thought. It’s possible that the job is not all we had hoped, or the investment carried more risk than expected.

As it turns out, differentiating between good deals and fair deals has significant implications for how much we bet on any given opportunity[1]. This begs the question: how do we identify good deals versus merely fair deals?

Here I propose a theory of risk-taking that borrows heavily from finance - so that’s where I’ll start.

defining our terms #

We start with Greek letters.

Alpha is the percent return above some arbitrary but remotely relevant benchmark. For example, if all the competitors in our sector had an annual return of 10%, we could reasonably argue that our own return of 14% suggests an alpha of 4%.

Alpha represents relative outperformance while negative alpha represents relative underperformance. In both directions, alpha diverges from some benchmark measure of normal.

“Normal” or “average” is an important point that I will revisit in a bit.

Beta, on the other hand, is a fairly complex term to define in its technical sense. In fact, you can’t even talk about beta without implicitly invoking the capital asset pricing model (CAPM), for which there is a vexing amount of theory to understand. I won’t attempt to crudely duplicate that here.

But this finance framing above is really just an entry point for something which I think is ultimately much more useful: how to abstract these concepts into other domains. Fortunately alpha and beta have intuitive correlates in our everyday lives because, at the end of the day, we all deal with risk.

actually beta #

Beta represents a type of risk you can’t diversify away. If you participate in anything risky at all, you are immediately exposed to this systematic risk. It’s risk that’s common to all of your investments, or common to everyone in your line of work, or common to everything generally, no matter what.

If you’re starting a business, it’s the risk that interest rates rise or the economy tanks or consumer demand weakens. No degree of diversification or project planning or enlightened stock picking can protect you. You could say that these risks - collectively, beta - are table stakes: you must shoulder them just to play the game[2].

In theory, more risk is compensated with more return. Similarly, the level of systematic risk or beta that is borne also earns some proportional level of return. We can call that return beta return: the return that the average investor is compensated just for playing the game and bearing systematic risk[3].

actually alpha #

Alpha, unlike beta, is not a measure of risk - it is a measure of return. It is the return in excess of the beta return. If the average entrepreneur bore some risk in starting a business and earned a return of 5%, while your competing business returned 8%, you delivered an alpha of 3% given the same level of systematic risk (again, everyone bears this, including you).

Positive alpha is an economic free lunch - for the same level of systematic risk, you outperformed the average investor’s beta return.

inefficient markets #

Alpha is always found in inefficient markets. Inefficient markets exist when there is some barrier or inefficiency causing assets to be mispriced, for example:

• people don’t have enough information to know the price should be different.
• there are patents, licenses or other regulatory barriers to entry.
• there isn’t enough capital flowing in to actually transact on these mispricings.
• there are anticompetitive phenomena, such as monopolies, which prevent others from taking advantage of mispricings more fully.

In all of these cases, there are two necessary and sufficient conditions for alpha capture:

1. There exists a mispricing due to market inefficiency.
2. Some investor, proprietor or trader actually trades and capitalizes on that mispricing.

Neither condition alone is sufficient: if the market is completely efficient, there is no way to extract alpha no matter how clever you are. Similarly, if mispricings do exist, you must actually take the risk and trade on them in order to capture that alpha.

information and informed investors #

As I mentioned above, markets can be inefficient for various reasons, but I will only focus on one in this post: information asymmetry. In inefficient markets with information asymmetry, alpha can be captured simply by having more information than other market participants. Or, using our two conditions above:

1. You have an informational edge over other market participants
2. You use that information to seize the mispricing opportunity (e.g. undervalued investment, business opportunity, arbitrage trade, etc.)

A classic example of an informational edge is insider trading: some people have more information (received from an insider) about a company than others, trade on it in advance of others knowing about it, and then generate an excess return when the price later moves.

Legal informational edges include knowing about a major public works project before others (e.g. new hospital downtown), using statistical models to predict price movements, or employing mosaic theory to understand a firm more deeply than others.

Investors with an informational edge are called informed investors, while everyone else is called uninformed investors. Informed investors are able to generate alpha in inefficient markets for the same level of systematic risk borne by uninformed investors.

the risk-preference payoff matrix #

And now with all the groundwork adequately laid, I arrive at my thesis.

We can apply that same understanding of alpha, beta, inefficient markets and informed investors to all the risks we take, not just those in finance.

In any competitive activity, every individual is exposed to beta. Be it financial markets or job markets or dating markets, there are exogenous, systematic factors which affect the range of outcomes for every individual, no matter who they are. These are table stakes.

And, on average, people will receive returns commensurate with these non-diversifiable risks. These are beta returns: the returns the average person (uninformed investor) gets for playing the game.

But, as with all things, there will also be people who know how to do these activities better and therefore have an informational edge. They could have a better network, or work more productively, or have specialized domain knowledge. These informed participants earn more than the beta return: they earn alpha.

Almost.

Informed investors can’t just know more - knowing without doing is meaningless - they have to actually do those things in order to capture the alpha. Informed investors can’t just stay in the house - they need to dial up their risk exposure to capture that alpha. In other words, they must be risk-seeking.

This payoff matrix illustrates my point:

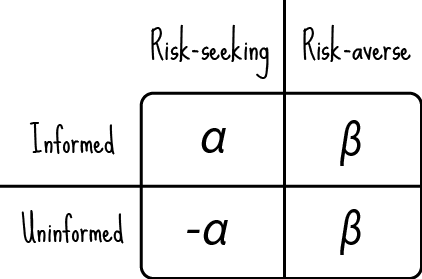
uninformed investors #

Unlike the informed investor, the “average, uninformed investor” should stick to beta. This means: don’t assume more risk than the average person. When you don’t have any informational edge, don’t stray from the beaten path! The uninformed investor should be risk-averse, take only beta risk and receive beta returns.

If you are uninformed, but are risk-seeking in search of alpha, you will fail. Think of the pollyannaish Silicon Valley entrepreneur who thinks she has the best startup idea ever (informational edge in market opportunities), but ultimately learns that her informational edge was no edge at all - she only ended up wasting her time and money. Negative alpha.

This is probably where those “most new businesses fail” statistics come into play: those who were uninformed but risk-seeking sought alpha, should have stuck to beta, and ultimately earned negative alpha. In all likelihood, either there was no alpha to begin with (market was efficient) or truly informed investors already captured those opportunities.

I am not suggesting that being uninformed is a bad thing - it is not. It is simply the state of your knowledge about a specific domain or opportunity - and if it’s not better than the average, you should stick to beta. For the vast majority of us, for the vast majority of things, we are uninformed.

informed investors #

On the other hand, informed investors should bear risk because they will be compensated not only with beta, but the alpha returns commensurate with their informational edge. It is one thing to be smart; it is another other thing to have courage to trade on that smartness. If you are convinced you have an amazing idea or trading strategy or investment opportunity, you must have the courage to actually pursue it if you want to realize that alpha[4].

Otherwise, we find ourselves at the top-right of the matrix: informed and risk-averse. You are forgoing alpha in favor of beta - that is, leaving alpha on the table. This is very common: intelligent, capable, competent (collectively, informed) people leave alpha on the table all the time because they don’t want to shoulder risk.

And there is nothing wrong with this! Real people have real-world commitments (eg. family, health, safety net, existing debt) which limit how much risk they can take. This strategy earns beta returns for a beta risk.

to be or not to be informed #

The remaining question is: are we informed?

Of course, everyone who pursues alpha thinks they have an edge (e.g. they’re smarter, more driven, more connected, etc.). If they didn’t, they wouldn’t prosecute that opportunity to begin with.

A priori, there are two analytical frameworks we could use:

1. We could say that the inside view - looking at just our own experiences - always tells us that we are uniquely situated to a seize an opportunity[5]. Which is also to say that the inside view is at least an incomplete, and sometimes unreliable, source of information.
2. We could also use the outside view: how have others like me fared in the past?

We tend to lean toward the inside view when we believe the data is wrong (i.e. sample doesn’t apply to us) or the model is wrong (i.e. game has structurally changed) - and conversely the outside view when they do apply.

If the outside view reveals that others have failed, this may not be such a tantalizing opportunity after all. On the other hand, if the outside view suggests others have fared well by playing the game you’re getting into, just how much alpha is left?

As a result, the outside view can only be a negative heuristic: it either tells us not to pursue an opportunity because others have failed, or because others have succeeded and already captured the alpha.

The only a priori green light must be the inside view.

a better way forward #

Fortunately we need not dive in head first with a priori estimations. We can (and should) test if we’re informed and if the market is inefficient.

Developers call this agile, entrepreneurs call it fail fast often - the concept has similar roots. Test the idea, generate actual data and see if the alpha is there. Only through this iterative process can we reliably determine whether an opportunity is the right opportunity for us, and if so, just how much risk we should take.

[1] Mathematically, this is the Kelly Criterion.
[2] I recognize I’m deviating from the CAPM theoretical definition of systematic risk (where every example I used is something you can actually diversify away) but I stretch the definition to illustrate a point.
[3] I think conceptualizing risk as a distribution again proves useful here. “Systematic risk” is the distribution (ie. a random variable) of all possible returns facing the average investor, and “beta return” is simply the mean of that distribution.
[4] Or, as Ray Dalio says: “There are only two things that one has to do to be successful: know what the best decisions are, and then have the courage to make them.”
[5] From Michael Mauboussin’s The Base Rate Book.