If something is "risky", consider its distribution

As someone who is generally risk-seeking, I am quick to expound on the benefits of taking risk. Of course I don’t see my actions as particularly risky in light of my particular circumstances, but I could probably do a better job of incorporating the outside view.

However as I reflected on risk-aversion more generally, I recognized a few reasons why it makes a lot of sense.

in defense of risk-aversion #

1. Volatility in outcomes erodes long-term returns due to compounding. If you have an equal chance of $0 and $10, getting $0 a couple of times in a row means no compounding those rounds. By contrast, $5 every time will always compound.

2. Many processes are path-dependent in time, meaning today’s outcome depends in part on yesterday’s outcome. If you go double-or-nothing at the casino (or in the stock market), then get nothing, there is no next turn. Do not pass go, do not collect $200. Nassim Taleb calls this the “risk of ruin.” If there is any risk of ruin (the worst of which is death), it is extremely rational to avoid these situations should you want another turn.

3. If the next $100 is less important to you than the last $100, then you exhibit diminishing marginal utility (DMU) of money. Restated, if the last $100 is more important to you than the next $100, then losing that last $100 must be more important to you than gaining the next $100. That idea took me a second to understand, so it’s worth re-reading. Finally, if we exhibit DMU, then we would rationally overweight losses relative to gains and avoid certainty-equivalent bets - in other words, we would be risk-averse.

in search of risk #

That being said, I still am able to justify (read: rationalize) my tendency to prefer risk:

• Risk is often perceived as a standard normal distribution (zero mean, unit variance) because that’s what we’re taught in school; however, this is rarely the case in the real world. Some distributions barely cross below zero, others have long negative tails (“black swans”), while yet others are power-law shaped. Here are some common distributions:

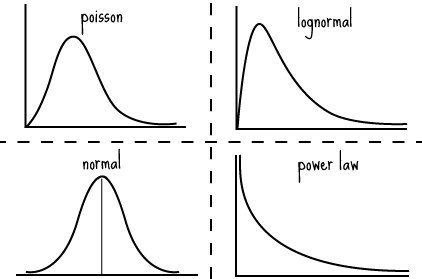
• If we’re dealing with something like a Poisson or power-law distribution (doesn’t cross below zero), then we want to be exposed to the “risk” of positive outliers. These outliers are non-linear in nature, event-driven and “gappy” in frequency (relative to the predictable nature of lower, more probable returns). These outliers have an outsize effect during compounding (i.e. reinvestment of these huge positive returns).
• If we don’t face the risk of ruin (your definition of “ruin” may differ), then we shouldn’t irrationally fear not having another turn.

As with most things, the answer is “it depends.” I think risk preference depends a lot on the distribution of risk you’re facing, but since I rarely perceive the risk of ruin and I see most real-life situations as positively skewed, I lean in to risk.

For more about risk, I recommend Patrick O’Shaughnessy’s interview with Jeremiah Lowin, who had an insightful comment that “Return is the draw from the distribution that risk is trying to model.”